NÚMEROS REALES
NÚMEROS REALES
Números naturales (N) : son aquellos que nos permiten contar elementos de un determinado conjunto. Gracias a esto, cuando realizamos operaciones con ellos los resultados pueden ser o no números naturales
Números enteros (Z) : diremos que el conjunto de los números enteros es igual de los números naturales unido con sus negativos.
Números racionales (Q) : llamaremos conjunto de números naturales o conjunto de números fraccionarios, al conjunto de todas las expresiones del tipo ab, donde a y b son números enteros y b es diferente a 0.
Números irracionales (I) :un numero irracional es un numero que no se puede escribir en fracción, el decimal sigue para siempre sin repetirse.
NÚMEROS REALES (R) : el conjunto de números reales pertenece en matemáticas a la recta numérica que comprende a los números racionales y a los irracionales. esto quiere decir que incluyen a todos los números positivos y negativos, el símbolo 0, a los números que no pueden ser expresados mediante fracciones de dos enteros que tengan como denominador a números no nulos.

Cuando un conjunto de números es denso y cuando es discreto?
El conjunto de números naturales es discreto porque entre dos números naturales existe una cantidad finita de números naturales. Lo mismo ocurre con el conjunto de los enteros.
El conjunto de números racionales es denso porque entre dos números racionales hay infinitos números racionales.
Sucesiones
Podemos definir a una sucesión (o progresión) numérica como un conjunto de números ordenados. A cada uno de estos números los llamamos términos de la sucesión: a1 es el primer termino, a2 es el segundo termino, a3 el tercero... an es el n-esimo termino.
Características:
- En función del numero que tengan, las sucesiones pueden ser finitas o infinitas.
- Son crecientes si cada termino es mayor al anterior.
- Son aritméticas cuando cada termino es la suma del termino anterior mas un numero constante, al que llamamos diferencia y denotamos por d.
- Son geométricas cuando cada termino es el termino anterior multiplicado por un numero constante, al que llamamos razón y denotamos por r.
Formula general:
| SUCESIÓN ARITMÉTICA | |
|---|---|
Es de la forma
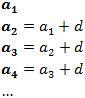 | |
Diferencia
|
Término general
|
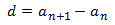 | 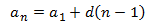 |
Suma de los n primeros términos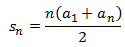 | |
| SUCESIÓN GEOMÉTRICA | |
Es de la forma
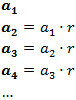 | |
Razón
|
Término general
|
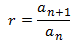 | 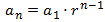 |
Suma de los n primeros términos
|
Suma de todos los términos
|
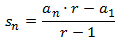 | 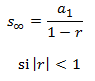 |
Intervalo
Es un conjunto de números reales que están ordenados de menor a mayor y se agrupan entre paréntesis o corchetes, por ejemplo:
(a;b); [a;b] donde a y b se conocen como valores extremos de intervalo.
Son regiones comprendidas entre dos números reales. En general, si los extremos pertenecen al intervalo, se dice que es cerrado, si por el contrario no pertenecen al intervalo, se dice que es abierto. Si uno de los dos extremos pertenece al conjunto y el otro no, se dice que es semiabierto y semis cerrado.
(a;b); [a;b] donde a y b se conocen como valores extremos de intervalo.
Son regiones comprendidas entre dos números reales. En general, si los extremos pertenecen al intervalo, se dice que es cerrado, si por el contrario no pertenecen al intervalo, se dice que es abierto. Si uno de los dos extremos pertenece al conjunto y el otro no, se dice que es semiabierto y semis cerrado.

Desigualdad
Es una expresión matemática que involucra los símbolos < > . La solución de una desigualdad es el conjunto de valores que hace de la misma una expresión verdadera. La solución de una desigualdad se puede expresar en forma de intervalo, conjunto y gráfica.
Valor absoluto
el valor absoluto o módulo de un número real es su valor numérico sin tener en cuenta su signo, sea este positivo (+) o negativo (-). Así, por ejemplo, 3 es el valor absoluto de +3 y de -3.
El concepto de valor absoluto de un número real puede generalizarse a muchos otros objetos matemáticos, como son los cuaterniones, anillos ordenados, cuerpos o espacios vectoriales.
Propiedad de la radicación
La raíz de un producto es igual al producto de las raíces de los factores nombrados anteriormente. Ejemplo:
Se llega a igual resultado que de la siguiente manera:
Formula para calcular el diámetro de la circunferencia:
2 . π . r
Formula para el área de una circunferencia:
NUMERO DE ORO:
El número áureo (también llamado número de oro, razón extrema y media, razón áurea, razón dorada, media áurea, proporción áurea y divina proporción) es un número irracional, representado por la letra griega φ (phi) (en minúscula) o Φ (Phi) (en mayúscula) en honor al escultor griego Fidias.
La ecuación se expresa de la siguiente manera:

Posee muchas propiedades interesantes y fue descubierto en la antigüedad, no como una expresión aritmética, sino como relación o proporción entre dos segmentos de una recta, es decir, una construcción geométrica. Esta proporción se encuentra tanto en algunas figuras geométricas como en la naturaleza: en las nervaduras de las hojas de algunos árboles, en el grosor de las ramas, en el caparazón de un caracol, en los flósculos de los girasoles, etc.
NUMERO PI

π (pi) es la relación entre la longitud de una circunferencia y su diámetro en geometría euclidiana. Es un número irracional y una de las constantes matemáticas más importantes. Se emplea frecuentemente en matemáticas, física e ingeniería. El valor numérico de π, truncado a sus primeras cifras, es el siguiente:

El valor de π se ha obtenido con diversas aproximaciones a lo largo de la historia, siendo una de las constantes matemáticas que más aparece en las ecuaciones de la física, junto con el número e. Cabe destacar que el cociente entre la longitud de cualquier circunferencia y la de su diámetro no es constante en geometrías no euclidianas.

Comentarios
Publicar un comentario